異なる記法で書かれた計算式から計算する/traverse

Tree-Diagram Tree-diagramによるinfix・postfix・prefix　notationの実現再帰によるin-order・pre-order・post-orderの走査実装あるTree-Diagramから特定のデータを持つノードを探索する前提 infix NotationからTree Diagramを構成する Stack Stack:dynamic memory allocation Search binsearch Queue(尻から入れて頭から出す) Recursion 再帰関数概論再帰における無駄な退避(waste withdraw)とは分割統治(Divide and Conquer)

Tree-Diagram

計算式は演算子(operator)と演算対象(object)の関係を記述しているにすぎない
- どの演算子にどの演算対象を渡すか
どのような記法であれ、この関係は維持される
木構造(グラフ)では共通したこれらの関係を示すことができる
infix-notation/postfix-notation/prefix-notationのいずれも、この関係のグラフ上をどのように走査し, 出力するかの違いにすぎない

Tree-diagramによるinfix・postfix・prefix　notationの実現

例えばinfix-notationで書かれた $(A+B)*(C+D)$ という数式における演算子と演算対象の関係は以下のようなツリーダイアグラムで示される。(グラフ理論的に言えば完全二分木)

(A+B)*(C+D)

graph TD
	P1((＋))--->A((A))
	P1((＋))--->B((B))
	P2((＋))--->C((C))
	P2((＋))--->D((D))
	
	Times((×))--->P1((＋))
	Times((×))--->P2((＋))

when the in-order it should be printed as infix notation

A+B*C+D

when the post-order it should be printed as postfix notation

AB+CD+*

when the pre-order it should be printed as prefix notation

*+AB+CD

再帰によるin-order・pre-order・post-orderの走査実装

単純な実装としてダイアグラム上のノードを再起的に見ていく.

つまり,

あるノードAに書かれたラベルを見る
- Aの右下に繋がれたノードBに書かれたラベルを見る
  - Bの右下に繋がれたノードCに書かれたラベルを見る.
    - Cの右下に繋がれたノードDに書かれたラベルを見る.
      - Dの右下に繋がれたノードEに書かれたラベルをみる.
        
        Eの右下に繋がれた…

というようなもの.

ここでは各ノードのデータは　rightとleftという二つのポインタを持つ.

right は自身に繋がれた右の子を指し示すポインタ, left は左の子を指し示すポインタである.

graph LR
node1(親)-->right(右の子)
node1(親)-->left(左の子)

the argument of the function is t2node type pointer p.

void intraverse (struct t2node *p)
{
    if (p != NULL) {
		  intraverse(p->left);
		  printf(“  %d”, p->data);
		  intraverse(p->right);
    }
}

graph TD
	subgraph main
		plus#1((＋))--->A((A))
		plus#1((＋))--->B((B))
		plus#2((＋))--->C((C))
		plus#2((＋))--->D((D))
		times((×))--->plus#1
		times((×))--->plus#2
	end
	
	subgraph STEP3
	subgraph STEP2
	subgraph STEP1 
		op#*((×))--> op#+[＋] 
	end
	  op#+((＋))--> num#A[A] 
  end
	    num#A[A] -->null[[NULL]]
  end

*を指すポインタpを用意する.
intraverse(p→left)が呼び出される.(1階層目 : pは* p→leftは+)
1. 関数にとってpは+を指していて, これはNULLではない
2. intraverse(p→left)が呼び出される.(2階層目 : pは+ p→leftはA)
  1. pはAを指していて, これはNULLポインターではない
  2. intraverse(p→left)が呼び出される.(3階層目 : pはA p→leftはNULL)
    1. pはNULLなのでifの中身が実行されずに一個前の再帰に戻る.
    2. この時, pはNULL, p→leftなどない
  3. この再帰におけるp→dataとはAを指す.よってprint(A)
    1. intraverse(p→right)が呼び出される.(3階層目 : pはA p→rightはNULL)
    以下同様

あるTree-Diagramから特定のデータを持つノードを探索する

計算量は

O(log(n))

前提

Tree-Diagramがn個のノードを持つとする.
- 完全二分木
  証明
  1. 高さがhの完全二分木のノード数は $n=2^k$ である
  2. よって両辺の対数を取ることによって.
  $\log_2 n= h\sim最悪時間計算量$
  
  Q.E.D
  1. 探索する対象の数はほとんど木の高さである.

infix NotationからTree Diagramを構成する

graph TD
        0x150704140((*))-->0x1507040c0((+))
        0x150704140((*))-->0x150704120((+))
        0x1507040c0((+))-->0x150704080((A))
        0x1507040c0((+))-->0x1507040a0((B))
        0x150704120((+))-->0x1507040e0((C))
        0x150704120((+))-->0x150704100((D))

# AB+CD-

Stack

Stack:dynamic memory allocation

#include <stdio.h>
#include <stdlib.h>
struct stack
{
    int *bd;
    int pt;
    int mx;
};

struct stack *initStack(int stack_size)
{
    struct stack *s;
    s = (struct stack *)malloc(sizeof(s));
    s->bd = (int *)malloc(stack_size * sizeof(int));
    s->pt = -1;
    s->mx = stack_size;
    return s;
}

struct stack *push(int v, struct stack *s)
{
    //++(s->pt);
    s->bd[++(s->pt)] = v;
    return s;
}

struct stack *pop(struct stack *s)
{
    return s->bd[(s->pt)--];
}

Search

binsearch

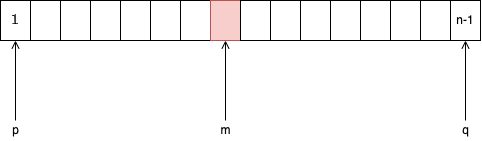
if v[m]>key then:
	/*-----  右を探索せよ ------*/
elseif v[m]<key then:
	/*-----  左を探索せよ ------*/
end

if-else構文の条件判定は配列の中を探索しているわけではなく, あくまでそれより大きいか小さいかを考えているだけであることに注意せよ.

Queue(尻から入れて頭から出す)

💡

QueueはFIFO(First In First Out)型のデータ構造, StackはLIFO(Last In First Out)型のデータ構造

struct queue{
	int bd;
	int mx;
	int hd;
	int tl;
}

struct queue *q;

struct queue* enqueue(int v,struct queue*q){
	q->bd[q->tl]=v;
	q->tl=(q->tl+1)%q->mx;
	
	return q;
}

int dequeue(struct queue* q){
	int v=q->bd[q->hd];
	q->hd=(q->hd+1)%q->mx;
	return v;
}

void status(struct queue*q){
	if(q->hd==q->tl)
		printf("Empty");
	if(q->hd=(q->tl+1))
		printf("Full");
}

Recursion

再帰関数

再帰を使って実現できるプログラムは非再帰で実現可能である.

pretraverse

void pretraverse(){
		struct stack *stck=newStack(stack_size, stack_name);
		push(p,stck);
		
		while(!isempty(stck)){
				p=pop(stck);
				printf("%d",p->data);
			  if (p->right != NULL)
		      push(p->right, s);
			  if (p->left != NULL)
		      push(p->left, s);	
		}

}

非再帰版のpretraverse関数

inorder (少し難しい)
postorder (少し難しい)

概論

再帰及び非再帰でもStackを利用していることに注意せよ. OSレベルで見ると再帰版はcall命令, 非再帰版は分岐命令, 一般にはcall命令の方が遅い.

よく設計された(well-designed)なアルゴリズムならば非再帰の方がわずかに早い.

再帰における無駄な退避(waste withdraw)とは

再帰
関数が呼ばれるたびに引数はシステムのスタックに積まれる.
例えば, 再帰関数Funcが10回目に呼び出された時だけ変数に対して処理をする…ということをすると
- 変数は宣言された時に領域を確保するので
```
void func(void){
	int i;
	
	if(cnt==10){
		/*処理1*/
		/*処理2*/
		/*処理3*/
		/*処理4*/
	}
	func();
}
```

分割統治(Divide and Conquer)

フィボナッチ数列の処理の場合
- 再帰版はおよそ $O(2^n)$
- 非再帰版は $O(n)$
  - 左の処理は右の処理と独立である

graph TD
        0x140704100((*))-->0x1407040c0((+))
        0x140704100((*))-->0x1407040e0((C))
        0x1407040c0((+))-->0x140704080((A))
        0x1407040c0((+))-->0x1407040a0((B))

graph TD
	A --> B
	B --> C
	A --> C

yunoki blog